Project: Reliable Multiscale Simulation
The objective of this research is to develop new physics-based data-driven mechanisms to quantify model-form and parameter uncertainties in multiscale systems simulation so that reliability and robustness of predictions can be assessed efficiently.
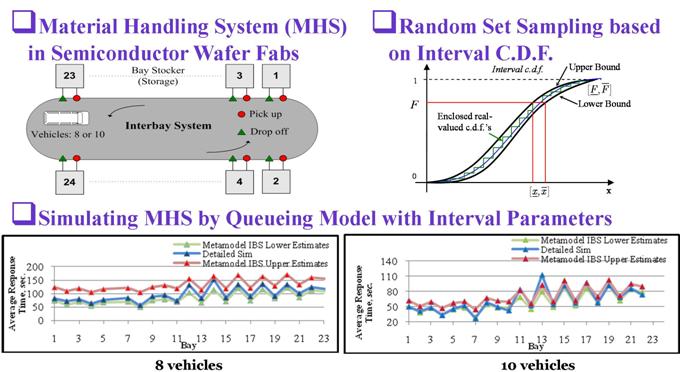
Metamodel of Queueing Systems
Distributions with interval-valued parameters are used to simulate queueing systems where the effects of model errrors on outputs can be assessed. The model errors include those from lack of data, inaccurate model forms, imprecise prarameters, unknown dependency relationships, and others. Metamodeling is based on random set sampling and many scenarios are simulated simultaneously. Therefore it can save computational time for both detailed fine-grained simulation and sensitivity analysis.
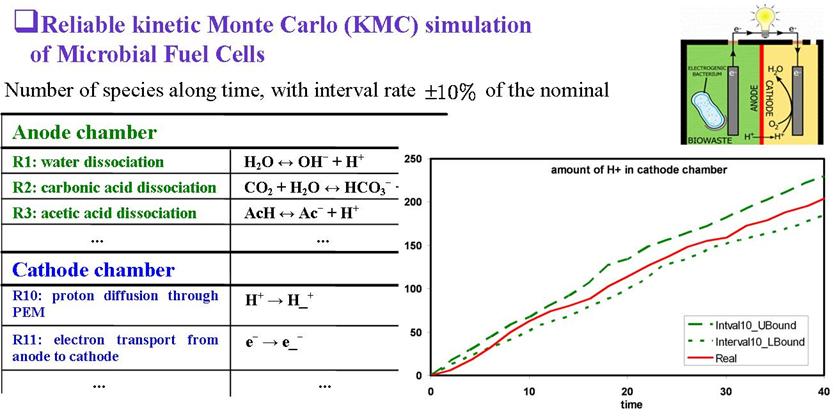
Reliable Kinetic Monte Carlo (R-KMC) Simulation
Random sets replace random numbers in kinetic Monte Carlo (kMC) simulation so that the dynamics of discrete physical and chemical systems can be simulated based on lower and upper probabilities. A multi-event algorithm is developed to choose either one or two events to occur at a time in R-KMC. It rigorously preserves the semantics of interval probability. The lower and upper bounds of times for clock advancement are predicted.
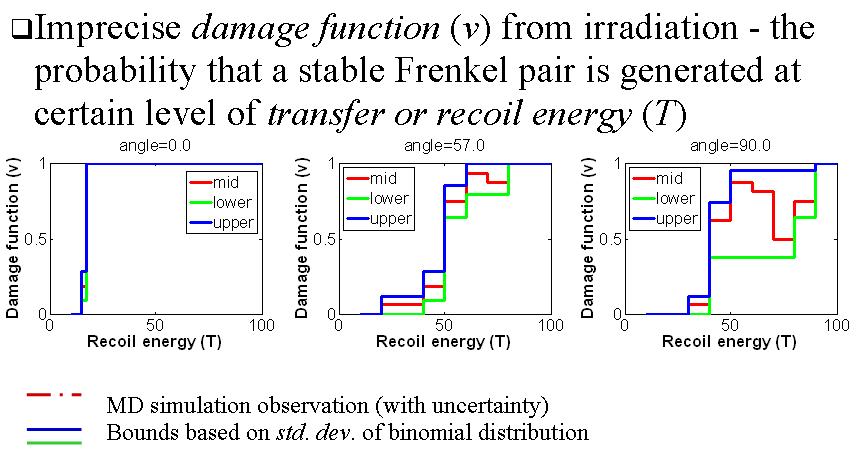
Reliable Molecular Dynamics (R-MD) Simulation
The model form uncertainty of molecular dynamics (MD) simulation is captured so that the epistemic uncertainty of prediction is quantified. Interval probability is used to describe the statistics of macroscopic properties. A new cross-scale validation procedure for MD models is developed.
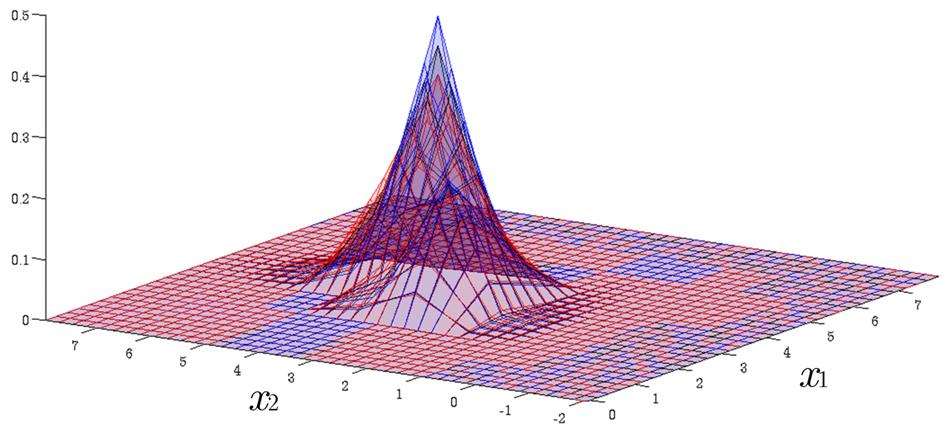
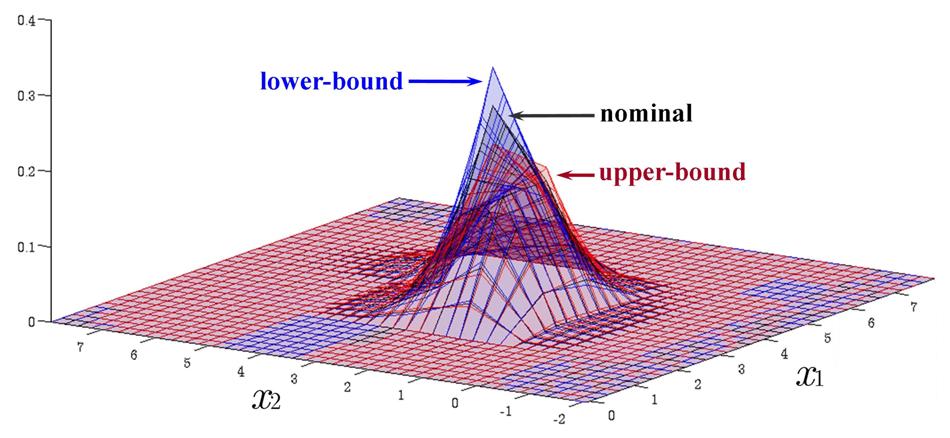
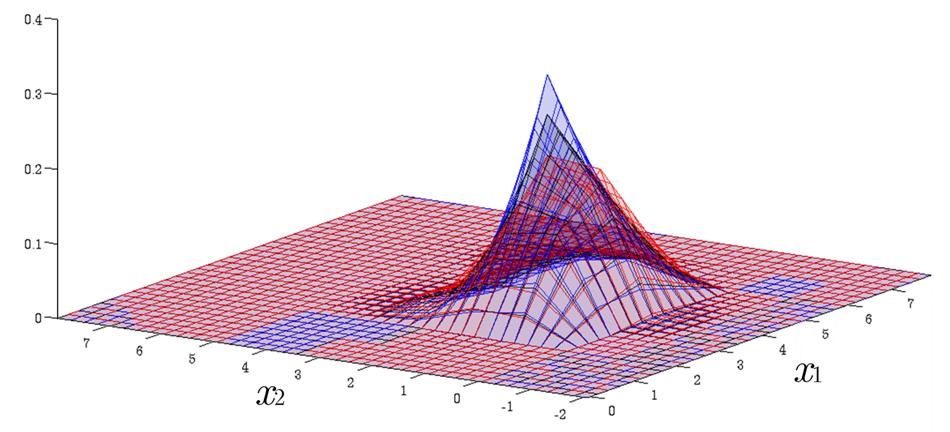
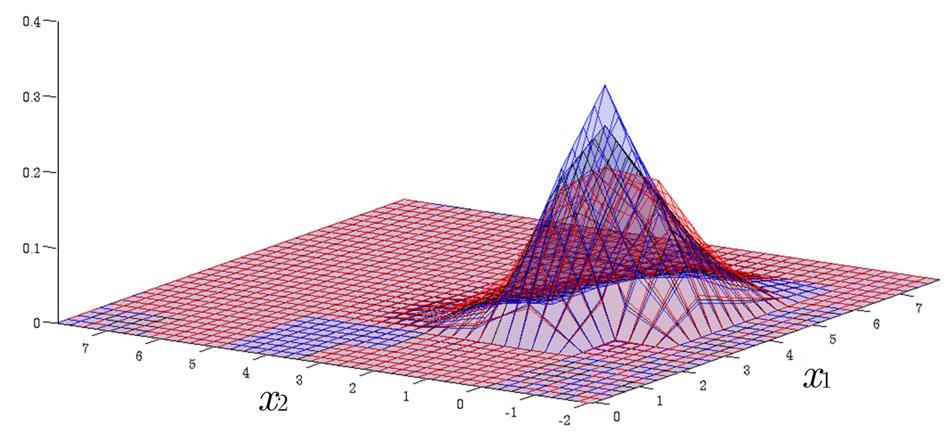
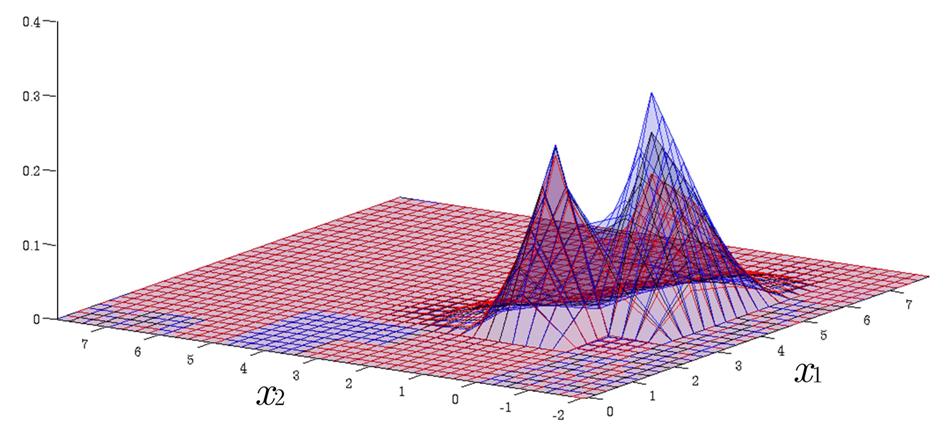
Time Evolution of Interval Probability Distribution
Generalized Fokker-Planck and interval master equations are developed to simulate diffusion and jump processes respectively under uncertainties. The estimated lower and upper probability densities are evolved simultaneously. Therefore, the traditional sensitivity analysis can be saved in assessing the effect of input parameters on the output results.