Project: Quantified Constraint Satisfaction Problem (QCSP)
The objective of this research is to develop hybrid numerical and logic reasoning approaches to solve constraint satisfaction problem with generalized interval.
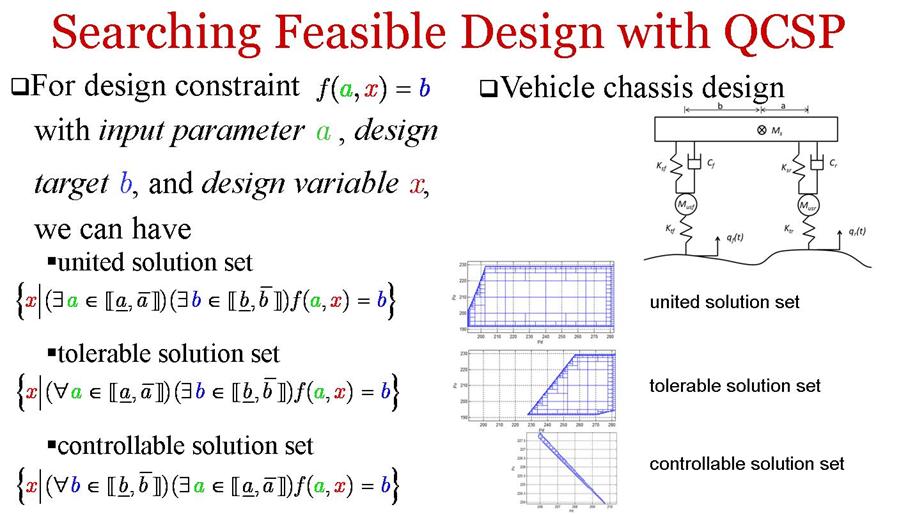
Feasible Design Space Exploration
In design of complex systems where multidisciplinary constraints are imposed by stakeholders, engineers need to search feasible solutions for a given design problem before the optimal one. A new approach to formulate searching feasible design problems as QCSPs based on generalized interval is developed. With the lower and upper bounds of design variables specified, feasible solution sets can be found numerically by solving interval constraints.
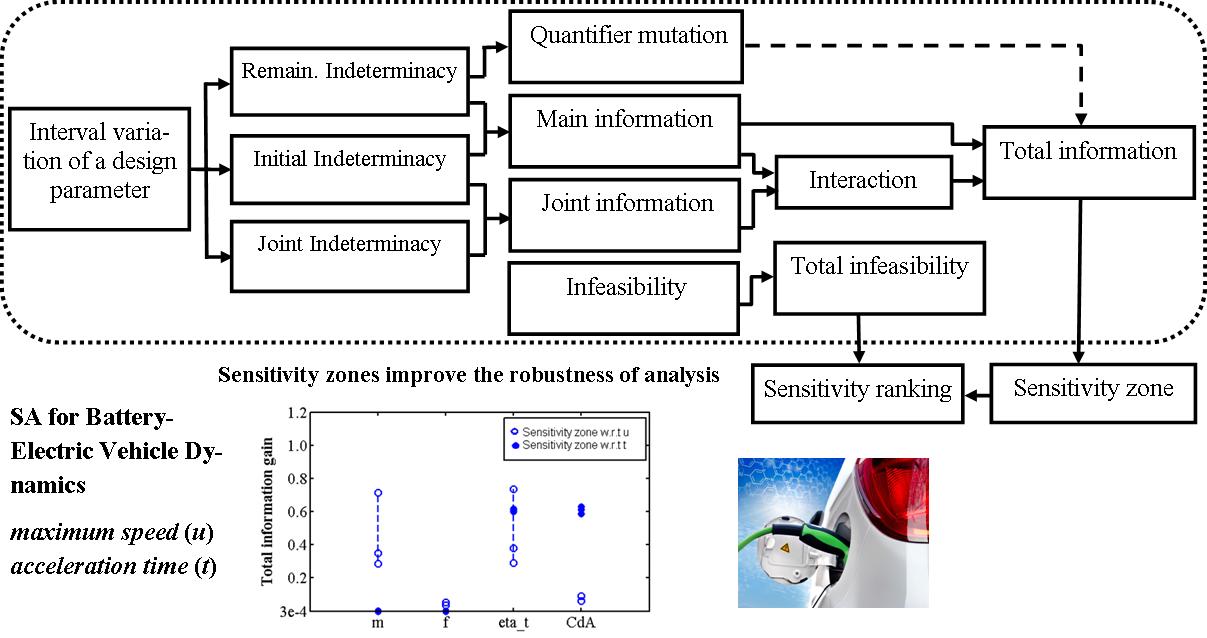
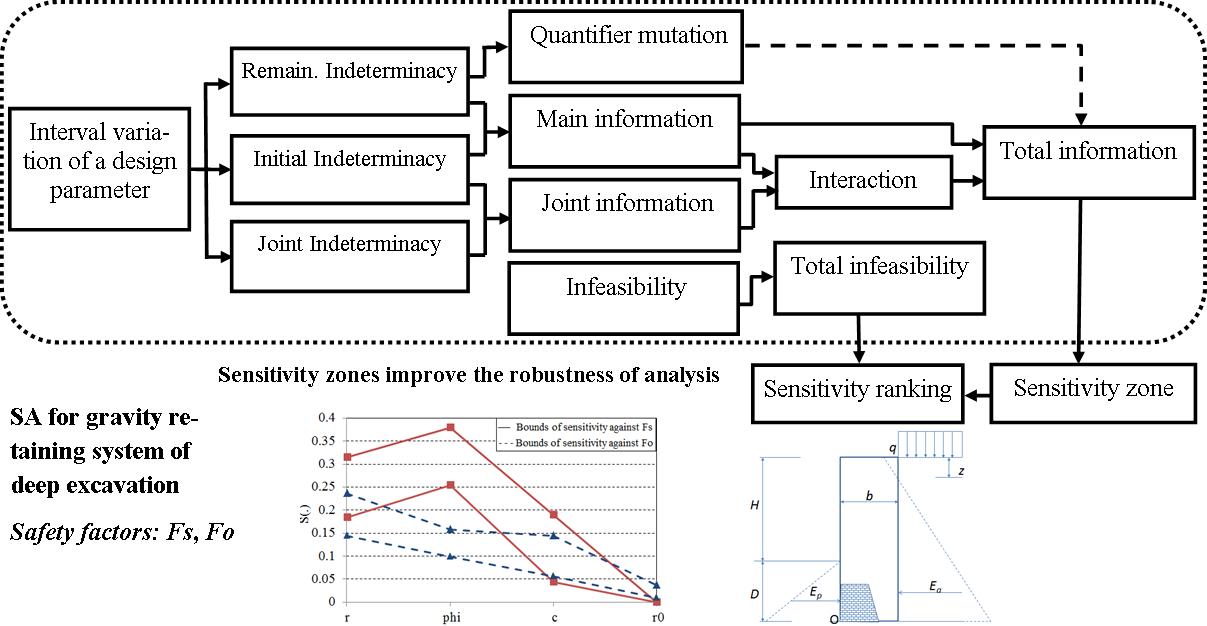
Global Sensitivity Analysis with Interval Uncertainty
A unique way to assess the sensitivity of input parameters is developed, where no assumption of probability distributions is needed and both individual and joint effects of interval uncertainty are incorporated. Additionally, the sensitivities of logic quantifiers associated QCSPs can also be evaluated.
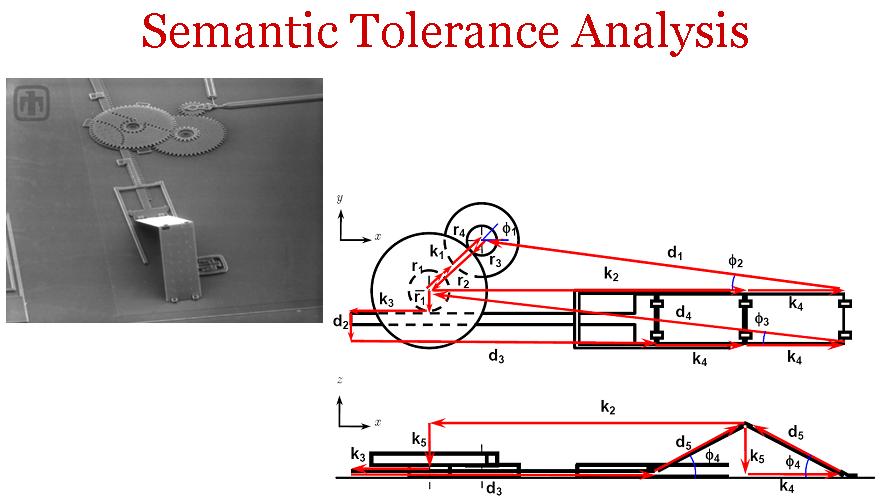
Semantic Tolerancing
Dimensional and geometric tolerances are typically specified as intervals to improve manufacturability, reduce costs, and ensure functionality. Yet the traditional tolerancing system only focuses on product whereas process related semantics is missing. Logic interpretability of generalized interval provides more power to encode process-oriented semantics in tolerance specification, with the differentiation of prior and posterior tolerances. Tolerance analysis problems are formulated as QCSPs. Numerical algorithms are developed to solve these problems.