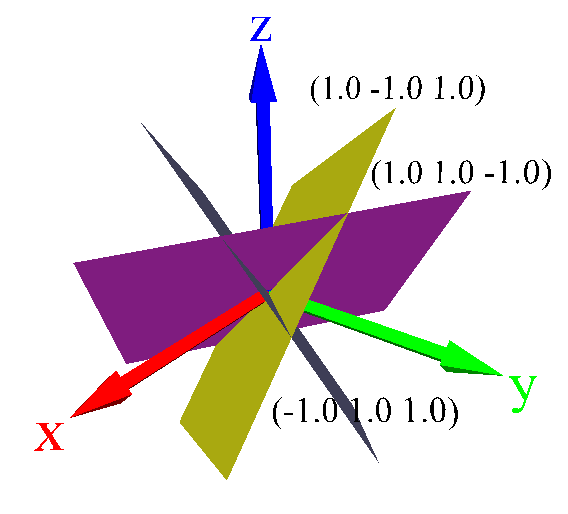Project: Computational Materials Design
The objective of this research is to develop new geometric modeling methods and efficient searching and optimization algorithms to enable computational materials design at multiple scales.
Geometric Modeling for Interactive Design
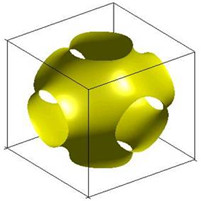
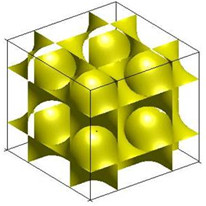
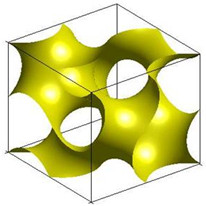
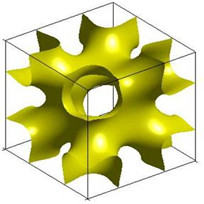
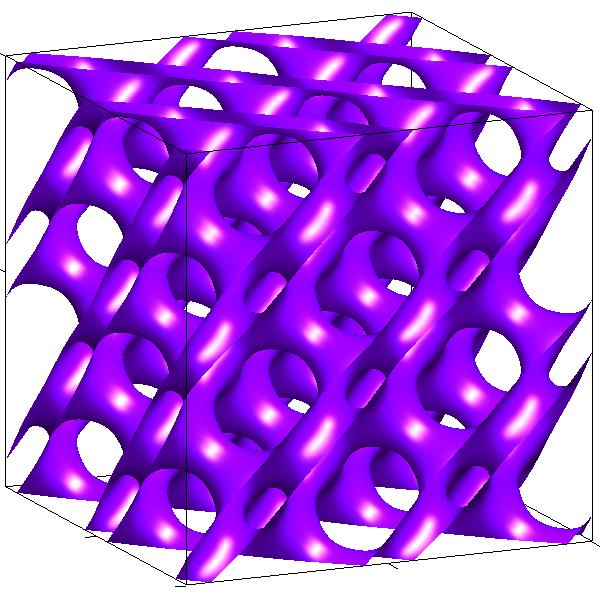
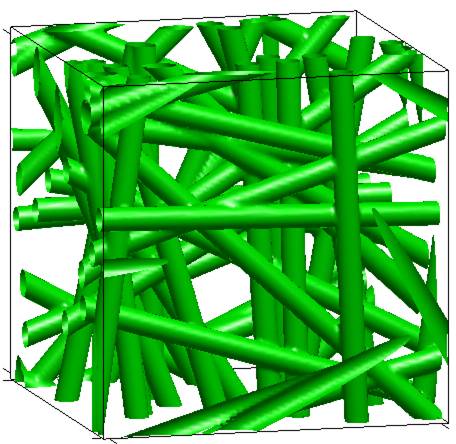
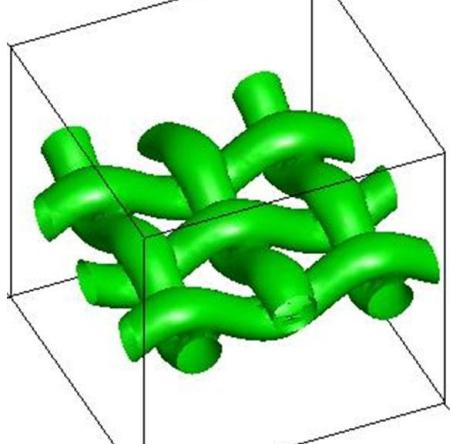
Providing engineers and scientists efficient and easy-to-use tools to create complex and super-porous geometry conformations that have minimum energies is highly desirable in materials design. We proposed a new periodic surface (PS) modeling concept to design and engineer complex structures parametrically including triply periodic minimal surfaces (TPMS) and fibrous porous media.
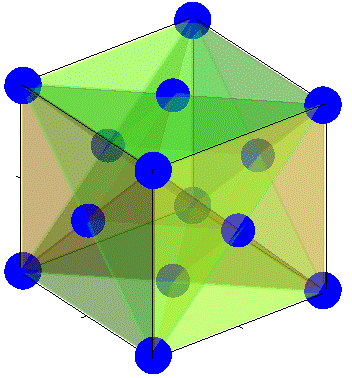
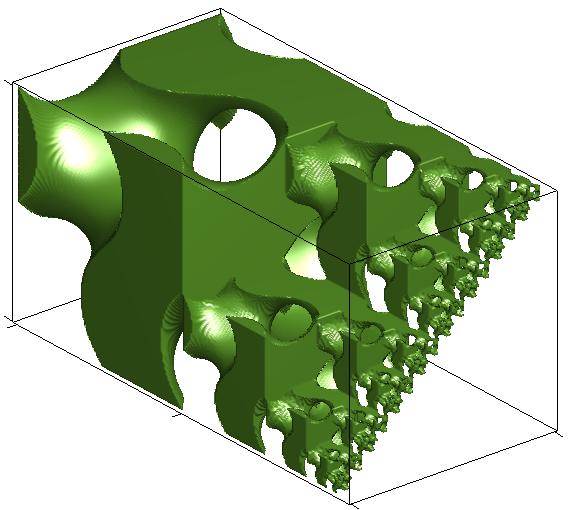
Methodologies to support interactive modeling such as Boolean operations, transformation, degree elevation and reduction, Minkowski sum, fractal structures, and feature-based crystal construction have been developed.
Our pioneering periodic surface modeling approach has now been widely adopted by researchers and engineers world-wide in designing additively manufactured cellulose structures and scaffolds as well as porous media.
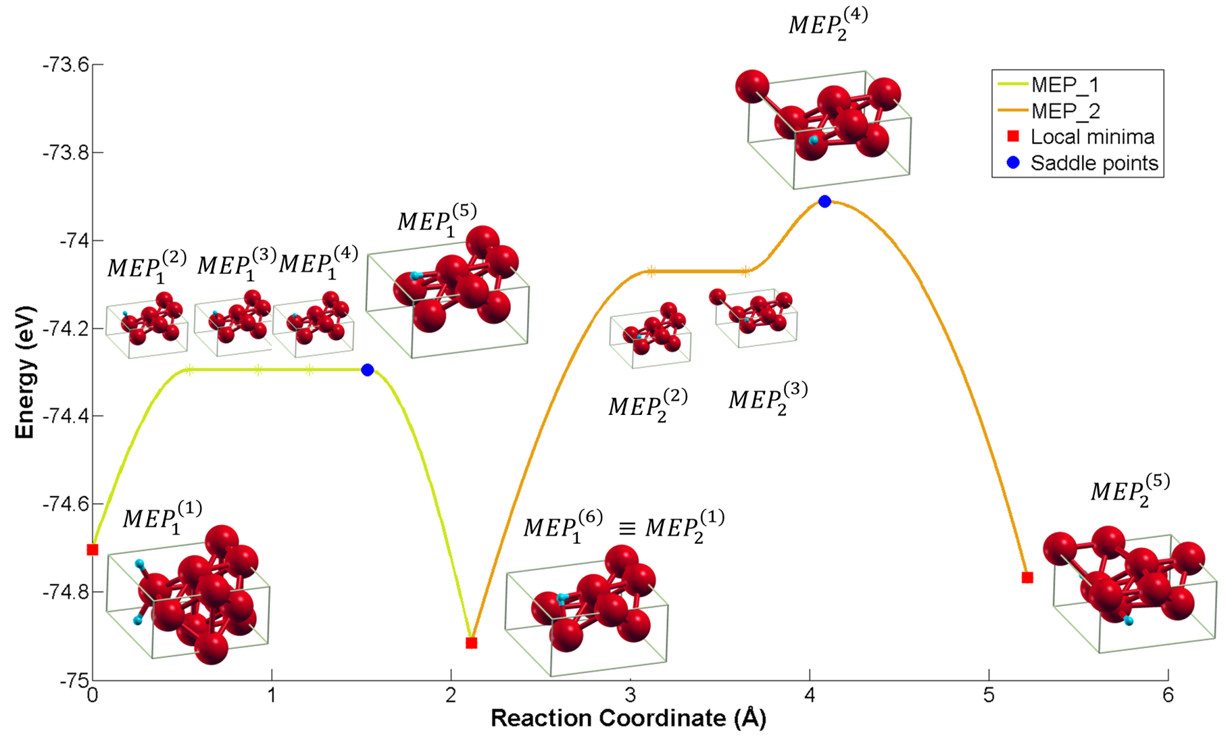
Saddle Point Search for Phase-Change Materials Design
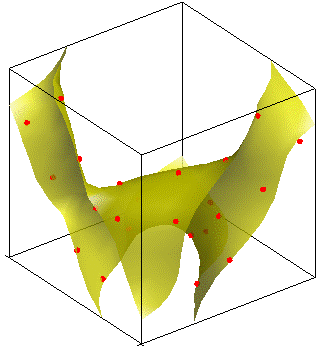
Searching first-order saddle points and minimal energy path on the potential energy surface (PES) is important to determine the activiation energy for phase transition. The accurate estimation of activation energy is critical for phase-change materials design, such as for energy storage (battery, Hydrogen storage, shape-memory alloy) and information storage (phase-change memory, CD-ROM), as well as the study of aging process and stability of materials and neucleation of defects, even protein-folding and endocytosis. The challenge is to accurately locate the saddle point with the minimum energy pathway in the very rough landscape of PES.
We developed a surrogate-based saddle point search method, where a Gaussian process regression model is constructed based on first-principles density-functional theory calculations. We also developed a curve swarm algorithm to search saddle point globally on complex and very high dimensional PES.
Bayesian Optimization for Materials Design
Design is an iterative searching process of identifying the feasible solutions that satisfy the design contraints and choosing the optimum from the feasible ones. The essential task of materials design is to establish process-structure-property relationships. Given the high-dimensional design space which can include many possible combinations of compositions and microstructures, the use of efficient global optimization algorithms is important.
In this research, we developed new scalable Bayesian optimization algorithms that support multi-fidelity and multi-objective optimization with mixed-integer design variables. We have applied these algorithms in designing metamaterials, battery configurations, biodegrable polymers, scaffolds, heart valves, etc.